Welcome to the Feature Column

---

Inside-out Frieze Symmetries in Ancient Peruvian Weavings

Posted October 2008.

In this column I plan to examine frieze symmetries as manifested in woven strips...

 

Tony Phillips
Stony Brook University
tony at math.sunysb.edu

 

Mail to a friend

Print this article

 

Background

The pre-Columbian civilizations of Peru had no written language and, as far as we know, no formal mathematics beyond the still inscrutable recording of information by patterns of knots in strings called quipu. But thanks to their custom of burying large quantities of textiles with their dead, and to the unusual aridity of the coastal area in central and south central Peru, many of their woven, embroidered or painted textiles have been preserved. The intricate symmetries of the decoration bear witness to the pre-numerical mathematical genius of these peoples, and give us a rare window into cultures which were first superseded by the Incas and then extirpated in the aftermath of the Conquest (1532).

Branko Grünbaum (see References, below) has analyzed the Peruvian exploitation of planar symmetries in textile decoration. In this column I plan to examine frieze symmetries as manifested in woven strips, and especially the uniquely Peruvian device of using double- and multiple-weaving to create an additional symmetry between the front and the back of a textile. Some of the textiles I am using as examples can be assumed to date from the "Late Intermediate Period" (1000-1400 AD) and to originate in the central or south-central coast. Adele Cahlander shows several similar examples which are reputably dated and sited. For others (the first and second groups below) I have not been able to find such exact published parallels. They are certainly pre-Inca and from that part of Peru.

Frieze symmetries

Frieze symmetries (the possible symmetries of a 1-dimensional strip of decoration) were completely analyzed (Speiser, Pólya, Niggli, 1924) in the early twentieth century. There are 7 possibilities:

1. FFFFFFFF (T: translation)
2. bpbpbpbp (TG: translation and glide reflection)
3. EEEEEEEE (THG: translation, up-down mirror symmetry, glide reflection)
4. TTTTTTTT (TV: translation and left-right mirror symmetry)
5. ZZZZZZZZ (TR: translation and 180-degree rotation)
6. bdpqbdpq (TRVG: translation, 180-degree rotation, left-right mirror symmetry, glide reflection)
7. HHHHHHHH (TRHVG: translation, 180-degree rotation, up-down and left-right mirror symmetry, glide reflection)

 

Double weaving

Double-weaving is a widespread technique which allows decoration of both sides of a textile at once. In the most common form, warp-faced double weaving, the warps for a cloth are set up on the loom with two yarns of complementary color in each position. The fabric is woven as usual by leading the weft over and under the warps, but here at each intersection the weft passes over one color and under the other. The result is that the two sides of the fabric bear mirror-image designs in opposite colors.

Double weaving and frieze symmetries

The ancient Peruvians combined double weaving and pattern symmetry, using color as an extra variable, to achieve symmetries between the two sides of a textile.

Suppose that a strip is double-woven with dark green and orange so that on one side ("recto") it shows the frieze pattern p p p p p p ... . The other side ("verso") will then show b b b b b b ... , i.e. the pattern from the recto, translated one step and reflected.

Here is an example:

 

Frieze symmetry T implemented in double weaving (width of decoration: 34mm). The color substitution from front to back corresponds to the translation. Therefore the back decoration is a (reversed) translated copy of the front.

This principle was exploited with more complex frieze symmetries:

 

Frieze symmetry TG implemented in double weaving (width of decoration: 21mm). Whenever the symmetry involves the glide-reflection G, then the pattern on the verso exactly replicates that on the recto after a translation.

 

 

Frieze symmetry TVG implemented in double weaving (width of decoration: 18mm).

 

 

Frieze symmetry TRVG implemented in double weaving (width of decoration: 28mm).

 

Multiple weaving with three colors

A singular achievement of the Peruvian weavers (I do not believe this was duplicated by any other civilization) was the production of textiles in which more than two yarns occupy each warp position. In ordinary cloth this is impossible, because one yarn is up, one is down and there is no place for others. The Peruvians solved the problem by using two sets of wefts: at each intersection one warp would go over the top weft, one warp would go under the bottom weft, and the rest would be hidden inside the double fabric so constructed. (In practice, a single weft was led across on the top and back on the bottom; the resulting very sturdy but bulky construction, aptly described by d'Harcourt as "tubular," was only used for belts and straps).

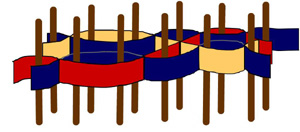
Here, as in the examples, blue is used as a background with two additional colors, yellow and red; four warps are strung in each position: two blues, one red, one yellow. In the diagram the wefts run vertically, with one set shown in front and one in back. The blue appears outside or inside simultaneously in front and in back, but yellow and red alternate.

 

         

 

Frieze symmetries T (width 40mm), TG, TVG (width 42mm) implemented with three warp colors (two working colors and one background). A band similar in size and construction, but with non-zoomorphic designs, is illustrated in Cahlander, Figs 5-6a,b; it is described as a "Nasca 'turban,'" which would date it around 500 AD.

Multiple weaving with four colors

With four colors typically one (usually red) is used as a background color and three others work the design. This extremely complex work was usually reserved for the backstraps the weavers themselves used to maintain tension in their looms. A specimen similar to this example, with the simpler T inside-out symmetry, is in the collection of the American Museum of Natural History 41.2/5104 (shown in Cahlander); another with TVG color-coded front-back symmetry (undoubtedly; Cahlander shows only one side) is in the collection of the Lowie Museum of Anthropology, University of California, Berkeley E13-1-3969.

 

Frieze symmetry TR, implemented in four-color multiple-warp weaving (width of decoration: 50mm). Here the working colors are blue, yellow and green. The white paper clip is a reference point.

The pattern in this example is the superposition of two two-color patterns, each with color-coded translation-rotation symmetry:

   

In the yellow-green pattern, interchanging yellow and green corresponds to a 180-degree rotation. Similarly for the blue-green pattern. In the weaving of this textile, the green in the yellow-green pattern is matched by yellow in the verso (and the yellow by green), whereas the green in the blue-green pattern is matched by blue (and the blue by green). In this way the entire front-back color substitution corresponds to a 180-degree rotation, and the verso shows the recto pattern translated, reflected and rotated by 180 degrees.

Since reflection in the longitudinal axis and rotation by 180 degrees is equivalent to reflection in the transversal axis, we can appreciate the phenomenon by giving the image of the recto an additional transversal reflection:

 

Note the position of the paper clip. When the image of the verso is flipped across a transversal axis, it exhibits the same pattern as the recto (up to a translation). The juxtaposition shows up a couple of small errors in the weaving.

References:

Adele Cahlander with Suzanne Baizermann, "Double-Woven Treasures from Old Peru," Dos Tejedoras, St. Paul MN 1985.

Raoul d'Harcourt, Textiles of Ancient Peru and their Techniques, University of Washington Press, Seattle, Washington and London 1962.

Branko Grünbaum, "Periodic Ornamentation of the Fabric Plane: Lessons from Peruvian Fabrics," Symmetry, 1 (1990) 45-68.

Anthony Phillips, "Simmetrie fronte-retro in manufatti tessili del periodo pre-Inca," in Matematica e Cultura 2007 (M. Emmer, ed.) Springer-Verlag Italia 2007 (an expanded version of much of this material).

 

Tony Phillips
Stony Brook University
tony at math.sunysb.edu

Those who can access JSTOR can find some of the papers mentioned above there. For those with access, the American Mathematical Society's MathSciNet can be used to get additional bibliographic information and reviews of some these materials. Some of the items above can be accessed via the ACM Portal , which also provides bibliographic services.