archimedes4The Method of Archimedes
4. The plane geometry behind the argument
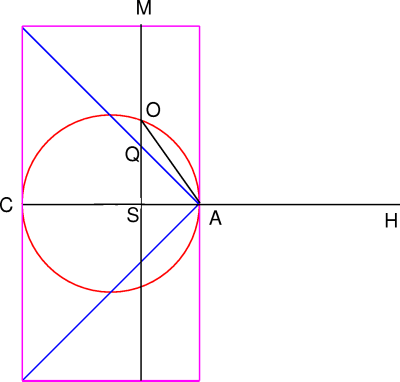
The areas of the three discs in question are proportional tothe square of their radii. With points labeled as in this diagram(adapted from T. L. Heath, The Works of Archimedes withThe Method of Archimedes, Dover, New York), the equationm d = M D from the previous pagebecomes
MS2.SA = (OS2 + QS2).AH .
Since MS = CA and SQ = SA, we have MS.SQ = CA.SA . Now OS is the altitude of the right triangle OSA and therefore OS2 = CS.SA . The Pythagorean theorem applied to OSA gives OA2 = OS2 + SA2, so
OA2 = CS.SA + SA2 = CA.SA, yielding MS.SQ = OA2 = OS2 + SQ2.
Since AH = CA it follows that
AH/SA = CA/SA = MS/SQ (substitutingequals for equals) = MS2/MS.SQ = MS2/(OS2 + SQ2). Cross-multipling gives the desired equation.



