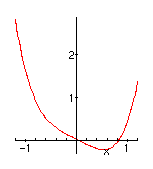
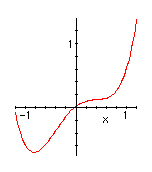
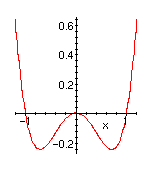
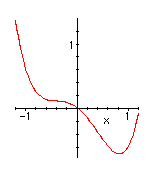
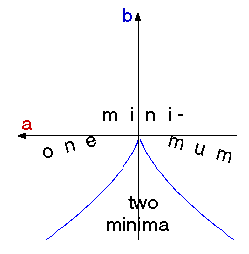
 | As in the fold case, the system will have a discontinuous response at points where a local minimum appears or disappears. A little calculus shows that the system has a single minimum unless
-0.5443(-b)3/2 < a < 0.5443(-b)3/2.
When the discontinuity locus
a=+/- 0.5443(-b)3/2
is graphed in the control space, with coordinates a and b, the plot shows the cusp shape characteristic of this catastrophe. One way to understand the behavior of the system, in analogy withthe double well, is to say that the output must track the controls,staying on a surface "above" control space like the one shown atthe right. When the right-hand fold is approached from the left,or vice-versa, the output is forced to jump to the other sheet.The membrane in the middle corresponds to the local maximum and isinaccessible. |  |