
Who Wants to Be a Mathematician : Barry Mazur Gives Arnold Ross Lecture
"Myself and the students had a wonderful time at both the lecture and the game. It was really a great trip for all. Thank you for arranging such a nice event. I hope to be part of it in the future."
|
|
|
On November 1, more than 300 Massachusetts high school students and their teachers filled the Museum of Science auditorium to hear the 2007 Arnold Ross Lecture by Barry Mazur and see Who Wants to Be a Mathematician.
How many prime numbers are there?, Barry Mazur, Harvard University
 |
Glenn Stevens (Boston University), a former student of Mazur's and the past chair of the Arnold Ross Lecture Series Committee, introduced Mazur, calling him "one of the most influential mathematicians alive today." Stevens noted some of Mazur's accomplishments: getting a Ph.D. from Princeton University at the age of 21, winning the AMS Cole and Steele Prizes, and - as evidence of his wide-ranging interests - being elected to the American Philosophical Society.
Mazur introduced the topic of prime numbers with a story from Don Quixote in which Quixote asked a poet to write a poem with 17 lines. Because 17 is prime, the poet couldn't find a length for the poem's stanzas and was thus stymied. Mazur then showed Euclid's proof of the infinitude of the primes, demonstrated how the Sieve of Eratosthenes worked, and spoke a little about the Twin Primes Conjecture. Mazur pointed out that the conjecture is still undecided, as are many questions about primes, and explained to students that although they are accustomed to math being about answering questions, a good portion of mathematics is asking them.
The rest of the lecture dealt with the distribution of the primes, mostly with counting the number of primes up to a given number - for example, the number of primes less than 1000. On its face this is a discrete problem, but Mazur noted that continuous functions associated with Gauss and Riemann give very good approximations to the number of primes below a certain threshold and showed graphs (below) that supported this claim. In the graph immediately below, the continuous approximations are so close to the function that gives the actual number of primes (in blue), that they are indistinguishable from it.
 |
Above: Number of primes up to n, for n = 1 to 1000. (Graph by William Stein, courtesy of Barry Mazur.)
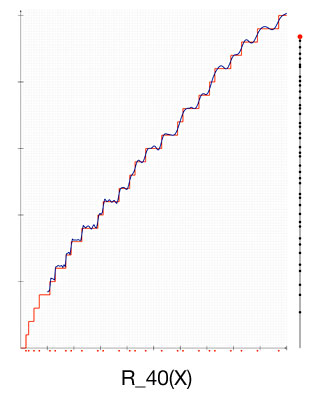 |
Above: One of Riemann's functions (blue) approximating the number of primes (in red). (Graph by William Stein, courtesy of Barry Mazur.)
 | The question-and-answer period that followed was very lively: Several students asked questions about topics such as formulas for primes and the largest known prime, both in the auditorium immediately after the lecture and just outside the auditorium during the break, and one teacher - Connie Varoudakis, who is also the assistant principal at Danvers High School - had Barry autograph her copy of his book, Imagining Numbers, Particularly the Square Root of Minus Fifteen. |  |
Who Wants to Be a Mathematician
Two very exciting games of Who Wants to Be a Mathematician followed the break. The contestants who played (pictured below) are (left to right):
- Eli Barrows, Waring High School
- John Avitable, Hanover High School
- Kristen Flannery, Notre Dame Academy
- Alex Bishop, St. Mark's School
- Mike Breen, AMS, host of Who Wants to Be a Mathematician
- Eric Holmquist, Mashpee High School
- Stephen Gutz, Danvers High School
- James Kingsley, St. John's Preparatory School
- Christine Chen, Westford Academy
|
Game one was very close throughout, and going into the last question, three students had a chance to win. James Kingsley was the only contestant to get the last question correct, which earned him a slot in the bonus round and a chance at $2000. Going into the last question of game two, three contestants also had a chance to win. In fact, all four contestants answered the last two questions (the most difficult questions in the game) correctly. Two of the contestants, Alex Bishop and Christine Chen, wound up tied for first place. Christine was the first to answer the tie-breaking question correctly and so she earned her way into the bonus round with James.
|
|
 | Both Christine and James thought and worked hard in the three minutes allotted to them, but unfortunately neither got the question correct. Although they didn't win the cash, they were still happy as they each won the new TI-Nspire graphing calculator. |  |
Here are the prizes won by all eight contestants:
- TI-Nspire graphing calculator from Texas Instruments: James Kingsley and Christine Chen
- Maple 11 from Maplesoft: Kristen Flannery and Alex Bishop
- Calculus by Anton, Bivens and Davis from John Wiley and Sons: Eric Holmquist and Eli Barrows
- What's Happening in the Mathematical Sciences from the AMS: John Avitable and Stephen Gutz
The AMS thanks Lynn Baum, Museum of Science, who made arrangements for the lecture and game; sponsors Texas Instruments, Maplesoft, and John Wiley and Sons for their continued generous support of Who Wants to Be a Mathematician; and the teachers who participated in this marvelous morning of mathematics.
Photographs by Who Wants to Be a Mathematician judge and co-creator Bill Butterworth (DePaul University Department of Mathematical Sciences) and by Robin Aguiar (AMS Meetings and Conferences).
Find out more about the Arnold Ross Lectures and Who Wants to Be aMathematician.







