
Thomas Hales Gives the 2010 Arnold Ross Lecture, Followed by Who Wants to Be a Mathematician
The Arnold Ross Lecture and Who Wants to Be a Mathematician traveled to the Carnegie Science Center in Pittsburgh, Pennsylvania on October 14 for an informative and exciting day of mathematics. A summary of the lecture and contest, including videos of the contest, is below.
"They had a great time playing and the rest of my class did playing along as well. We also enjoyed the lecture very much. The students I brought are all extremely interested in mathematics. They're all seniors from my Linear Algebra class, a very talented bunch who all passed BC Calculus last year, so they really enjoyed the day. I hope that you return to Pittsburgh soon!"
"Thank you for the excellent event. My students and I thoroughly enjoyed the lecture and the competition."
"Thank you for the opportunity for our student to participate in the “Who Wants to Be a Mathematician” game today. She and the rest of our students had a great time. We hope that you will be coming to our area again in the future. The day was a great experience for our students."

The 2010 Arnold Ross Lecture: Can Computers Do Math?, Thomas C. Hales, Andrew Mellon Professor of Mathematics, University of Pittsburgh
Hales talked about packing problems, giving their history and why they are important in modern mathematics and its applications.
His first example was packing tetrahedra, that is, putting them together to fill space. Aristotle thought that all of space could be filled by arranging tetrahedra so that five of the solids were arranged around every edge of each tetrahedron, but it turns out that that configuration leaves a small gap: The tetrahedra don't quite fit together, or fill space, as imagined.
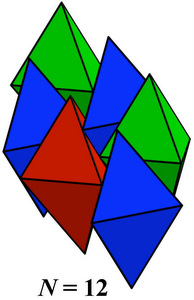 |
Recently, researchers have used computers to find a packing of tetrahedra that would use up the greatest percentage of space. One of those researchers is Elizabeth Chen, who purchased several packages of Dungeons and Dragons tetrahedral dice to help find the best packing. She found a packing that occupies more than 85% of space, but at this point it is not known if that is the best possible arrangement. Chen handed out packets of the dice at her dissertation defense. Her team of researchers includes a chemical engineer who has used the mathematical results to build molecular clusters for a rudimentary cloaking device. (Image from "Dense crystalline dimer packings of regular tetrahedra," Chen, Engel, Glotzer) |
Hales then moved to packing spheres. He showed what looked like two different arrangements of spheres--one tetrahedral and the other pyramidal (pictured, below left)--which turned out to be the same face-centered cubic arrangement (Hales is holding them together, below right), cut at different angles. This packing is familiar to many as it is often used in grocery stores to pack oranges, for example.
 |
 |
In the 1500s Sir Walter Raleigh wanted to know how many cannonballs were in the stacks in his ships. Hales showed the audience how Raleigh's advisor, Thomas Harriot, used what is known as Pascal's Triangle, to solve the problem. Although determining the most efficient method for packing the spheres is a 400-year old problem, it is used today in error-correcting codes, which are important in digitized media such as music.
Whether this face-centered cubic packing is the most efficient became known as the Kepler Conjecture and was undecided until Hales submitted a proof of this conjecture, which 12 referees examined over an 8-year period. At the end of this time they said that they were 99% sure that the proof was correct but could not be 100% sure, so he began trying to teach computers to do mathematical proofs. Hales showed the audience the journal issue that was his proof, which, although long, wasn't as long as others.
Hales concluded with another example that united a fairly old conjecture and modern mathematics. The question was how to divide space into cells of equal volume that have the least area of surface between them. Lord Kelvin thought that the cells were truncated octahedra. This was believed to be correct until 1994 when two physicists Phelan and Weaire discovered a counterexample (pictured below left). Their configuration served as the basis for the design of The Cube, the aquatics center at the 2008 Summer Olympics. Since then, many configurations better than Kelvin's (e.g., below right) have been found.
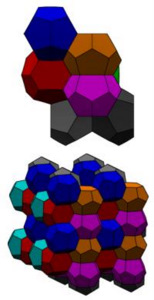 The Phelan-Weaire formula |
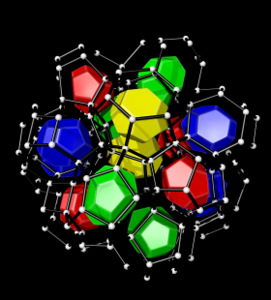 "P42" |
Who Wants to Be a Mathematician
 |
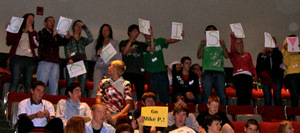 At left, rooting sections for Mike Panza and Michael Matty. Above: Chrissy's rooting section |
After the lecture and some nice refreshments, eight Pittsburgh-area high school students played Who Wants to Be a Mathematician. The big winners were Michael Matty of Pine-Richland High School and Chrissy Martin of Steel Valley High School, who won US$1000 and $500, respectively, from the AMS, and each won a TI-Nspire graphing calculator from Texas Instruments.
 |
Pictured, left to right: Kyle Berkow, Hampton High School; Mike Panza, Deer Lakes High School; Thomas Hales; Connor Brem, Mt. Lebanon High School; April Peng, Moon Area High School; Chrissy Martin, Steel Valley High School; Michael Matty, Pine-Richland High School; Maria Guadagnino, Mt. Lebanon High School; and Daniel Salmon, Shaler Area High School |
 |
Connor Brem led most of the way in game one, but Chrissy won the game by answering the last question correctly. (Front: Connor and Chrissy, Back: Mike and April)
|
 |
In game two, Michael Matty also led most of the way. Kyle Berkow pulled ahead after question six, with two questions to go. Going into the last question, the four contestants were within 800 points of one another, but Michael answer the last question correctly to win. (Front: Kyle and Maria, Back: Michael and Daniel)
|
 |
Then Chrissy and Michael, having each won $500 and a TI-Nspire, went head-to-head on the Square-Off Question for the right to be in the Bonus Round and perhaps earn $2000. The two contestants both missed on their first chance at the Square-Off Question, but Michael answered the question correctly on his second chance, which won him another $500. |
Unfortunately, Michael did not get the Bonus Question, which concerned three mutually tangent circles inscribe in a larger circle, but he and Chrissy still got paid the big bucks.

Here are all the prizes and money won that day.
- TI-Nspire graphing calculator from Texas Instruments and $1000 from the AMS: Michael Matty
- TI-Nspire graphing calculator from Texas Instruments and $500 from the AMS: Chrissy Martin
- Maple 14 from Maplesoft: Connor Brem and Daniel Salmon
- Calculus by Anton, Bivens and Davis from John Wiley and Sons: Kyle Berkow and Mike Panza
- What's Happening in the Mathematical Sciences from the AMS: April Peng and Maria Guadagnino
The AMS thanks sponsors Texas Instruments, Maplesoft, and John Wiley and Sons for their continued generous support of Who Wants to Be a Mathematician. Thanks also to the Carnegie Science Center for hosting the event and to the Pittsburgh area teachers and students who attended.

Steelers fans "don't need no stinkin' arrows."
Photographs by Who Wants to Be a Mathematician judge and co-creator Bill Butterworth (DePaul University Department of Mathematical Sciences), Robin Aguiar (Meetings and Professional Services), and by Who Wants to Be a Mathematician host and AMS Public Awareness Officer Mike Breen.
Find out more about the Arnold Ross Lecture series and Who Wants to Be a Mathematician.

