
Invited Addresses, Sessions, and Other Activities
Benjamin Pittman-Polletta, an assistant teaching professor at Drexel University and 2010 AMS-AAAS Media Fellow, and Claudia Clark, freelance science writer and 2003 AMS-AAAS Media Fellow, summarize some of the invited addresses and other talks presented at the 2011 Joint Mathematics Meetings. Also see the JMM2011 blog written by 2007 AMS- AAAS Media Fellow Adriana Salerno of Bates College.
* Modeling the evolution of "comfort behavior" in seabirds * Cyphering books in the early history of mathematics education in North America
* Photos from Chuu-Lian Terng's AMS-MAA Invited Address and Alexander Lubotzky's AMS Colloquium Lecture I
* Minicourse on math and music theory * Panel on research that has social justice applications
* More on math and social justice * Andrea Bertozzi's Invited Address on self-organization * U.S. presidents' math interests
* Modeling gang rivalries * Teaching elementary math * The philosophy of mathematics
A Darwinian dynamics model for the evolution of "comfort behavior" in seabirds, Shandelle M. Henson (Andrews University)
 Evolution is nothing if not thrifty, frequently “co-opting" traits evolved for one purpose by adapting them to new purposes. For example, feathers are thought to have evolved initially to serve as heat regulation in birds, only later being co-opted for flight. Henson, who spoke about “comfort behavior" in the SIAM Minisymposium on Applications of Difference and Differential Equations in Ecology and Epidemiology, set out to answer the question of how evolution repurposes physiological behaviors to serve psychological ends. More specifically, she wanted to know whether preening, a behavior serving the physiological need of keeping feathers in good condition, could evolve into a comfort behavior, alleviating stresses like those induced by passing predators.
Evolution is nothing if not thrifty, frequently “co-opting" traits evolved for one purpose by adapting them to new purposes. For example, feathers are thought to have evolved initially to serve as heat regulation in birds, only later being co-opted for flight. Henson, who spoke about “comfort behavior" in the SIAM Minisymposium on Applications of Difference and Differential Equations in Ecology and Epidemiology, set out to answer the question of how evolution repurposes physiological behaviors to serve psychological ends. More specifically, she wanted to know whether preening, a behavior serving the physiological need of keeping feathers in good condition, could evolve into a comfort behavior, alleviating stresses like those induced by passing predators.
In Henson's research, the fact that a behavior can be triggered by many different cues is key. “Take eating," she said, “one of my favorite examples." Eating behavior can be cued by hunger, by smelling food, or even by thirst, since many animals hydrate by eating. At the same time, no one of these cues elicits eating behavior all the time. The way an animal expresses a given behavior is characterized by a vector v, in which v i is an exponent determining the probability with which cue i produces the behavior.
In Henson's model, the value of v evolves to maximize a fitness function G(N; v) = b(v) - c(v) - d(v)N, which reflects the balance between the population's birth rate b(v), its death rate c(v), due to stresses such as exertion, and its density-dependent death rate due to crowding d(v)N. To model the evolution of a comfort behavior, Henson imagines that, to optimize individual fitness, the behavior should occur in response to n physiological cues (vi nonzero for i = 1,..., n), but not in response to an (n+1)st psychological cue (vn+1 = 0). She also assumes that if the behavior occurs in response to the psychological cue, it will decrease an individual's health, by decreasing b(v) and increasing c(v), but it will decrease the density-dependent death rate due to crowding d(v)N. This leads to the possibility of a trade-off, where using the behavior as a coping mechanism becomes adaptive even when it damages an individual's health.
Finally, Henson presented a preliminary field test of her theory. Preening is cued by humidity, temperature, isolation, wind, and tide, among other cues. Videotaping seabird populations, she was able to estimate the vi values for these cues. She then videotaped eagle disturbances of the populations, and found that preening increased slightly in these situations, estimating vn+1 was approximately 0.27. Thus, it's possible for preening as a comfort behavior to invade seabird populations.
---Benjamin Pittman-Polletta
SIGMAA on the History of Mathematics Guest Lecture: The special role of cyphering books in the early history of mathematics education in North America. M. A. Clements and Nerida F. Ellerton (Illinois State University)
 Clements and Ellerton began their presentation by describing a few of the highlights of their work with cyphering books—handwritten mathematics texts prepared by students using a teacher’s text. Since they first came across a cyphering book in 2005, Clements and Ellerton have collected over 200 American cyphering books, the earliest of which dates from 1701. Based upon their examination of over 500 cyphering books, they wrote and presented a paper in October 2010 in which they argue that these books were of fundamental importance in the history of mathematics education. However, their focus for this evening was to introduce the audience to cyphering books: describe what are, say a little about their history, and present images from several of these books, including 10 that they brought from their own collection. For example, they noted that a typical cyphering book "was dedicated to setting out mathematical definitions, rules, cases, model problems and their solutions, and exercises with solutions prepared by the person who owned the cyphering book." These books could contain problems from arithmetic, algebra, geometry, or trigonometry, particularly in relation to business. But perhaps the most noticeable characteristic of many of these books is the beautiful calligraphy. (The example is from a text dated 1702.) These books, sometimes subtitled "My Book," were clearly intended to be kept as references by the student, as "handbooks for life."
Clements and Ellerton began their presentation by describing a few of the highlights of their work with cyphering books—handwritten mathematics texts prepared by students using a teacher’s text. Since they first came across a cyphering book in 2005, Clements and Ellerton have collected over 200 American cyphering books, the earliest of which dates from 1701. Based upon their examination of over 500 cyphering books, they wrote and presented a paper in October 2010 in which they argue that these books were of fundamental importance in the history of mathematics education. However, their focus for this evening was to introduce the audience to cyphering books: describe what are, say a little about their history, and present images from several of these books, including 10 that they brought from their own collection. For example, they noted that a typical cyphering book "was dedicated to setting out mathematical definitions, rules, cases, model problems and their solutions, and exercises with solutions prepared by the person who owned the cyphering book." These books could contain problems from arithmetic, algebra, geometry, or trigonometry, particularly in relation to business. But perhaps the most noticeable characteristic of many of these books is the beautiful calligraphy. (The example is from a text dated 1702.) These books, sometimes subtitled "My Book," were clearly intended to be kept as references by the student, as "handbooks for life."
Interestingly, Clements and Ellerton have found that between 17 and 20% of the cyphering books they examined—including some which contained comparatively difficult topics—were prepared by girls. (Most historians have claimed that very few girls prepared cyphering books.) They also mentioned that cyphering books appear to have “died very suddenly” after 1860. To learn why they think this occurred, and to learn more about cyphering books, you can view a slide show of their October presentation, and keep an eye out for their upcoming book. (Image courtesy of Nerida Ellerton)
---Claudia Clark
Photos from AMS-MAA Invited Address "Curves, surfaces, and solitons,"by Chuu-Lian Terng (University of California, Irvine) and from Lecture I of the AMS Colloquium Lecture "Expander graphs in pure and applied mathematics," by Alexander Lubotzky (The Hebrew University of Jerusalem)
 |
 |
 |
 |
 |
 |
(Photos above by E. David Luria)
MAA Minicourse on Geometry and Algebra in Mathematical Music Theory: Part A, Dmitri Tymoczko (Princeton University)
For mathematicians like myself, who are more visual than musical, Dmitri Tymoczko's fascinating and accessible lecture provided deep insights into the world of music theory through the power of mathematics.
The lecture dealt with the geometry of musical structures, a subject Tymoczko expounds on at length in his new book, A Geometry of Music. This work, which could be thought of as a generative linguistics of standard music theory," attempts to use geometry to illuminate the underlying logical structure of music, and bring a uniform explanation to disparate musical phenomena. According to Tymoczko, one of the keys of this approach is thinking of musical notes as lying on a continuum rather than being discrete. "It wouldn't surprise mathematicians," he said, “to be told the continuous case is the easy one."
To get into the heart of the theory, think of a musical object, such as a chord, as a collection of notes. By assigning each note a pitch, we can identify the space of notes with a line, so musical objects are points in a Euclidean space. Tymoczko's theory deals with both musical objects and musical progressions, which are ordered pairs of musical objects, and can represent, for example, a "voice leading"--a direction for linking pairs of notes in two musical objects, so that the listener interpolates between them to perceive many "voices" rising and falling from one note to the next.
The geometry arises from the five so-called OPTIC symmetries that musical objects admit. For example, two notes whose frequencies are related by a factor of two are perceived to have the same pitch. This is called octave equivalence (O). Identifying notes which are an octave apart leads to a circular space of pitch classes, and an n-torus of n-note musical objects. A voice leading going from one note to another in the same pitch class can be distinguished from the constant voice leading by its winding number.
Altogether, there are five types of symmetries that musical objects admit:
- octave equivalence (O);
- permutation of notes (P);
- transposition or translation, adding a constant to all notes (T);
- inversion or reflection, subtracting all notes from a fixed number (I);
- and the tricky cardinality invariance, which allows notes to be duplicated (C).
Applying different combinations of these OPTIC symmetries to the space of n-note musical objects yields 32 different equivalence classes of musical objects, 18 of which are already known to music theorists.
Interesting geometries are obtained by considering the moduli spaces of these equivalence classes. For example, an n-note chord is an OP equivalence class of n-tuples of notes. Thus, the space of two-note chords is a Möbius strip - a two-torus with a twist, representing permutation invariance, and whose edges act as mirrors. The space of n-note chords is a twisted cylinder, whose cross-section is an (n - 1)-simplex, and whose top and bottom faces are identified after a cyclic permutation of vertices. An n-note chord type is an equivalence class of n-note objects under OPT. The space of three-note chord types is a cross-section of the space of 3-note chords--a triangle--whose edges are further identified, yielding a cone. Adding a scale to this musical data superimposes a lattice of possible notes onto the moduli space.
These symmetries can be applied to musical progressions as well, in two ways--either to each object in the progression individually, or to both objects simultaneously. The first is called an individual application, the second, uniform. For example, a chord progression is an equivalence class of musical progressions under individual applications of OP, while a voice leading is an equivalence class under uniform applications of OP. Altogether, there are 243 equivalence classes of musical progression. These musical geometries are not only interesting in their own right--they also help to understand the internal logic of various pieces of music. For example, on the cone of 3-note chord types, the chords which evenly divide the scale are located near the tip of the cone. Furthermore, there are three different routes between any two chords, allowing for many different melodic paths. Tymoczko also showed a video, available on his website, illustrating how a difficult-to-analyze piece of music by Chopin moves systematically through the hypercubic lattice of 4-note chord types. He noted, "Chopin really did understand the musical relationships that amount to a four-dimensional geometry," and invited us to marvel at a time when the most developed understanding of high-dimensional geometry was found not in math texts, but in the embodied knowledge of musicians.
---Benjamin Pittman-Polletta
AMS Panel Discussion: Proving Hardy wrong: Math research with social justice applications. Panelists: Lily Khadjavi (Loyola Marymount University) and Gizem Karaali (Pomona College); Organizer and moderator: Eva Curry (Acadia University)
The first speaker, Lily Khadjavi, described how she came to combine her interest in social justice with her love of mathematics, specifically number theory. At first, she focused on developing social justice materials for the classroom and doing outreach for underrepresented students. Then, a few years ago, while searching for real-world data for a statistics class she was teaching, she came across a data set online that "no one seemed to be analyzing": aggregated data on traffic stops made by the LAPD, tallied by race and ethnicity. Both Khadjavi and her students were "shocked" by what they found. After writing an article for Chance magazine about this work, Khadjavi was able to get the disaggregated data with the help of a law professor she knew and the ACLU. This collaboration has helped her to “tap into the appropriate conferences or venues or forums for this material.” She has attended and spoken at various legal conferences, reads a lot of law reviews and economics journals, has built a new research network, and has been able to find new funding sources. To others who would consider doing math research in the area of social justice, she would recommend a process similar to her own: Start small and build from there. She has found it very rewarding.
The next speaker was Gizem Karaali, who gave a presentation entitled "Mathematical approaches to the school districting problem." Karaali studied electrical engineering in college, then logic and representation theory in graduate school. In 2005, Karaali met another representation theorist, Julie Glass, at a geometric combinatorics workshop. After reading an article entitled "Rental Harmony: Sperner’s Lemma in Fair Division" in the American Mathematical Monthly, they decided to try applying Sperner’s lemma and fair division to the problem of how to divide the city of Oakland, CA, into school districts so that educational resources were allocated fairly. They wrestled with a variety of approaches but could not find one that was not lacking, so they took a more geometrical approach and looked at Voronoi distributions. Eventually another Monthly article, "College Admissions and the Stability of Marriage" by D. Gale and S. Shapley, caught their eye. This article proposed a particular algorithm, which has been applied in the school districts of a number of major cities, including Boston and New York. Eventually, Karaali and Glass wrote a paper—"A Cost-Minimizing Algorithm for School Choice"—that combines this algorithm with a few new criteria. (The article is currently in preprint.) At the end of her presentation, Karaali provided a list of journals—traditional and not-so-traditional—where a paper such as theirs might be published, including Discrete Applied Mathematics, Optimization, Mathematical Social Sciences, Social Choice & Welfare, and a new online journal with which Karaali is affiliated, the Journal of Humanistic Mathematics.
Although a third panelist, Judith Sunley of the National Science Foundation, was unable to attend, some of the work supported by the NSF—including work that addresses climate change, sustainability, control of disease, and health and wellness—was discussed. Links to information about these programs are included below.
Toward the end of the discussion, organizer Eva Curry asked the panel and members of the audience to describe what they would do if they were a graduate student and wanted to focus on social justice issues. Responses included: have a flexible advisor; look for contacts or mentors in other departments; consider interdisciplinary programs; look into schools with a social justice agenda; participate in summer programs, such as MSRI’s summer program on climate change; bring in your own funding; and take statistics courses!
For more information on NSF programs, check out the following websites:
www.mathinstitutes.org/climate-initiative/
www.mpe2013.org/
www.nsf.gov/sees
www.nsf.gov/dir/index.jsp?org=sbe and
www.nsf.gov/funding/pgm_summ.jsp?pims_id=503556&org=ARC
For information about a forthcoming website containing information about mathematics and social justice applications, contact eva.curry@acadiau.ca.
---Claudia Clark
Math and social justice: Improving the world with semester projects in a liberal arts math course, David Kung (St. Mary's College of Maryland), part of the MAA Session on the Mathematics of Sustainability
David Kung began his thought-provoking presentation with a vivid demonstration of how important mathematics is to functioning in modern society, by presenting opposing quotes from the 2008 presidential campaign. A quote from John McCain claimed that Obama's tax plan would increase taxes on 50% of small-business revenue, while a quote from then-Senator Obama claimed that 98% of small businesses would get a tax cut under his plan.
Kung went on to point out that nonmajor students need the quantitative skills to make sense of conflicting claims such as these, or to understand what it means to say that global temperatures and CO2 emissions are positively correlated with a correlation coefficient of 0.86. But what math departments offer them is something quite different: A choice between precalculus courses ("To what end?"), courses that teach "consumer math," and courses that provide the highlights of higher-level mathematics.
In his search for a better way to provide nonmajors with a positive last math course, Kung created the course "Survey of Mathematics: Math for Social Justice." Kung's goals for the course were not only to build his students' quantitative literacy, but also to give them a training in activism, and to give them the experience of making a concrete change in the world using the power of mathematics. His course description reads: "In this section of Survey we will use mathematics to better understand justice, fairness, and equality. Then we will use that new knowledge to improve the world."
The course covered mathematical topics including large numbers, percentages, statistics, distributions, surveys, voting, and financial mathematics. But the heart of the course was a semester-long project that students carried out in teams of two to four students. Each student came up with a project proposal, which had to address a social justice issue, use mathematics in a non-trivial way, be completed during the semester, and improve the world in some way. The class then voted on the ten best proposals--using a ranking system--and assigned teams to carry them out.
Some of the more successful projects included an attempt to provide solar water heating for student dormitories which garnered $30,000 worth of funding; a successful proposal to bring free-trade products to a local coffee shop; and an effort to establish a campus composting program which is slated to begin this fall. Just as exciting, reports Kung, the participants in the class were highly engaged, became better informed citizens, and improved their scores on a test of quantitative literacy by 23.8%--much more than participants in classes on the Millenium problems (-2.8%), or the mathematics of games (9.8%).
---Benjamin Pittman-Polletta
AMS Invited Address: Self-organization in human, biological, and artificial systems, Andrea Bertozzi (UCLA)
In what was surely the only talk at the Joint Meetings where the initials KAM stood not for Kolmogorov, Arnold, and Moser, but for the Krazy Ass Mexicans--a gang in Los Angeles' Hollenbeck neighborhood --Andrea Bertozzi (pictured below in a photo by E. David Luria) gave a whirlwind tour of research she and her collaborators have done into the emergence of complex collective behavior from the actions of individuals following simple rules.
 She began by discussing a variety of attempts to model criminal behavior like auto theft and gang violence, conducted in collaboration with UCLA criminologists and the LAPD. To study the occurrence of auto theft, Bertozzi and her collaborators define a function A(x; t) of space and time which indicates how "attractive" any particular spot is towards burglary events. The value of A controls both the probability that a burglar will move to an area, and the probability that a burglar will commit a crime in that area. The function A has both static and dynamic components, increasing whenever a crime occurs in a location, spreading to neighboring locations, and decaying over time. In simulation, both a discrete agent-based model and its continuum limit exhibit parameter regimes in which crime is uniformly distributed in space, and regimes in which “hotspots" of criminal activity form. Analysis of the continuum model shows that the nature of these hotspots varies. In the supercritical regime, these hotspots occur when the area of criminal activity is larger than the area over which A diffuses, so the diffusion of risk binds local crimes together. In the subcritical regime, different parameter values produce hotspots with an important qualitative difference: Some hotspots are extinguished by crime-suppressing police activity, while others merely re-form elsewhere. This dichotomy is known but not understood by police, and ripe for further investigation. One application of this work which has already materialized are estimates, based on real data, of the probability of a robbery occurring in a particular location in Hollenbeck. These estimates are made possible using a total variation minimization algorithm, which Bertozzi and her collaborators hope to patent.
She began by discussing a variety of attempts to model criminal behavior like auto theft and gang violence, conducted in collaboration with UCLA criminologists and the LAPD. To study the occurrence of auto theft, Bertozzi and her collaborators define a function A(x; t) of space and time which indicates how "attractive" any particular spot is towards burglary events. The value of A controls both the probability that a burglar will move to an area, and the probability that a burglar will commit a crime in that area. The function A has both static and dynamic components, increasing whenever a crime occurs in a location, spreading to neighboring locations, and decaying over time. In simulation, both a discrete agent-based model and its continuum limit exhibit parameter regimes in which crime is uniformly distributed in space, and regimes in which “hotspots" of criminal activity form. Analysis of the continuum model shows that the nature of these hotspots varies. In the supercritical regime, these hotspots occur when the area of criminal activity is larger than the area over which A diffuses, so the diffusion of risk binds local crimes together. In the subcritical regime, different parameter values produce hotspots with an important qualitative difference: Some hotspots are extinguished by crime-suppressing police activity, while others merely re-form elsewhere. This dichotomy is known but not understood by police, and ripe for further investigation. One application of this work which has already materialized are estimates, based on real data, of the probability of a robbery occurring in a particular location in Hollenbeck. These estimates are made possible using a total variation minimization algorithm, which Bertozzi and her collaborators hope to patent.
In the second part of her talk, Bertozzi discussed research into the temporal patterns of gang violence in Hollenbeck, between gangs with names like Hazard, Clover, and of course "KAM." "I didn't make this up," she said, “that's what they're called." She and her collaborators used a self-exciting point process to model the eruption of gang violence, coming to the counterintuitive conclusion that the eruption of one rivalry can trigger the eruption of a different rivalry, so that police should monitor all gang boundaries when any gang acts up.
Some of the same themes arose in the final part of Bertozzi's talk, in her discussion of swarming behavior in animals. Again, both agent-based and mean field models can be used to understand the formation of swarming patterns, such as vortex mills and clumping, which occur repeatedly in nature. Continuum limits produce differential equations which give rise to complicated patterns, including some which look like soccer balls, in what Bertozzi and her collaborators have dubbed "the World Cup Example."
---Benjamin Pittman-Polletta
AMS Session on History of Mathematics: Early American presidents’ mathematical interests, Andrew Perry (Springfield College)
Long before becoming the first United States president, George Washington learned and used mathematics. The death of his father brought Washington’s own formal education, which included Euclidean geometry, to an end when he was 15. A few years later, he would begin a successful career as a surveyor for Culpeper County in Virginia. The year before he became president, Washington wrote a letter to Nicolas Pike, author of the highly-regarded text "System of Arithmetick," which gives evidence of his admiration for the subject: "The science of figures, to a certain degree, is not only indispensably requisite in every walk of civilized [sic] life; but the investigation of mathematical truths accustoms the mind to method and correctness in reasoning, and is an employment peculiarly worthy of rational beings."
 In contrast to Washington, second U.S. president John Adams (at left) earned a college degree. During his short tenure as a schoolteacher, Adams wrote of his appreciation for and desire "to prosecute the mathematical and philosophical sciences." Several decades later, however, he would write to his wife Abigail, "I must study politics and war that my sons may have liberty to study mathematics and philosophy…" (His son and sixth U.S. president, John Quincy Adams, did study mathematics with his father before attending Harvard and would later propose a formula, the so-called Adams method of apportionment, for determining a state’s representation in Congress. It was never adopted.) Adams own library contained several serious mathematics texts, including Marquis de L’Hôpital’s Analyse des infiniment petits, which contains notes in Adam’s handwriting.
In contrast to Washington, second U.S. president John Adams (at left) earned a college degree. During his short tenure as a schoolteacher, Adams wrote of his appreciation for and desire "to prosecute the mathematical and philosophical sciences." Several decades later, however, he would write to his wife Abigail, "I must study politics and war that my sons may have liberty to study mathematics and philosophy…" (His son and sixth U.S. president, John Quincy Adams, did study mathematics with his father before attending Harvard and would later propose a formula, the so-called Adams method of apportionment, for determining a state’s representation in Congress. It was never adopted.) Adams own library contained several serious mathematics texts, including Marquis de L’Hôpital’s Analyse des infiniment petits, which contains notes in Adam’s handwriting.
Third U.S. president Thomas Jefferson also studied mathematics in college and enjoyed the subject throughout his life. Among his numerous accomplishments, he proposed his own formula for determining congressional representation, the so-called Jefferson method of apportionment. (It was used for over 50 years.) Jefferson also advocated for the use of a decimal currency and proposed the use of the metric system in the United States. He would also create a "wheel cipher" for encrypting information.
Based on pages from an early copybook, we know that 16th U.S. President Abraham Lincoln studied arithmetic as a child. According to an autobiography, Lincoln "studied and nearly mastered the Six-books of Euclid (geometry) since he was a member of Congress. He began a course of rigid mental discipline with the intent to improve his faculties, especially his powers of logic and language. Hence his fondness for Euclid, which he carried with him on the circuit till he could demonstrate with ease all the propositions in the six books…"
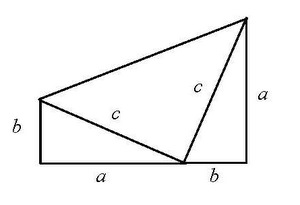 The final early U.S. president selected by Perry is the 20th, James Garfield, who graduated from Williams College in 1856. Garfield taught mathematics at Hiram College in Ohio. While a member of Congress, Garfield discovered a new proof of the Pythagorean Theorem, using the fact that in the diagram at left, the area of the trapezoid--(a + b)(a+b)/2--equals the sum of the areas of the triangles--ab/2 + ab/2 + c2/2.
The final early U.S. president selected by Perry is the 20th, James Garfield, who graduated from Williams College in 1856. Garfield taught mathematics at Hiram College in Ohio. While a member of Congress, Garfield discovered a new proof of the Pythagorean Theorem, using the fact that in the diagram at left, the area of the trapezoid--(a + b)(a+b)/2--equals the sum of the areas of the triangles--ab/2 + ab/2 + c2/2.
---Claudia Clark
An agent-based approach to modeling gang rivalries, Laura M. Smith (UCLA)
For those who didn't get their fill of L.A. gangs at Andrea Bertozzi's invited address (summarized above), Laura Smith's presentation in the AMS Special Session on Self-Organization in Human, Biological and Artificial Systems provided another chance to understand the network of gang rivalries in Hollenbeck. Smith described attempts to model the formation of gang rivalries, and to reproduce the network of 69 rivalries between Hollenbeck's 29 gangs, using several methods in network analysis. The first of these was a graph-generating method. The edge between two gangs was weighted by the product of their size divided by the distance between the gangs' home turf. Then, a weight threshold was chosen to produce exactly 69 rivalries. In two agent-based methods, gang members were allowed to wander independently and randomly through a discrete model of Hollenbeck, incorporating freeways and other geographical features as semipermeable boundaries. Whenever members of two gangs encountered each other, an interaction was recorded. At the end of the simulation, rivalries between gangs who had a mutually insignificant number of interactions were excluded. Gang members' wanderings were modeled in two ways: as a Brownian walk, and as a biased Lévy walk. The biased Lévy walk was chosen to reflect research suggesting that when people move in an unconstrained environment, the "jump lengths" obey a power law, and criminologists' suggestion that gang members tend to head towards their own territory. The graph-generating method yielded a network of rivalries markedly different from the known network. The agent-based network modeling gang members as Brownian walkers yielded an overconnected network. Modeling gang members as biased Lévy walkers resulted in a graph whose statistics best matched that of the known gang rivalry network.
---Benjamin Pittman-Polletta
AMS Committee on Education Panel Discussion: Teaching elementary math is not elementary: How mathematicians can help, and why? Moderator: Lawrence Gray (University of Minnesota); Panelists: Kenneth I. Gross (University of Vermont), Johnette Roberts (City of Baker, LA School System), Hyman Bass (University of Michigan), and Kristin Umland (University of New Mexico)
After introducing the panelists, Lawrence Gray presented Kenneth Gross’s material. (Gross was unable to attend.) Gross is the creator of the Vermont Mathematics Initiative (VMI), part of which is a three-year master’s degree program for elementary and middle school teachers. The program consists of 13 math courses, including trigonometry, probability, number theory, statistics, and calculus. Gross thinks that it important to teach "real" math to elementary school teachers because what is taught at this level provides a foundation for everything else. For example, "how can a student understand the derivative if they don’t understand subtraction and division?" Gray asked. "How can a student understand the integral if they don’t understand addition and multiplication?" In fact, "the area model used by elementary school teachers for multiplication is the same model used to explain what a Riemann sum is. If that connection is never made by teacher, it won’t be made by the students." So far, the program has had a positive impact: "a six-year quantitative evaluation study shows significant growth in student achievement and a narrowing of the achievement gap for students from low income families," Gray noted.
 The next presenter, Johnette Roberts, is the site coordinator of the Singapore Math Project for kindergarten through third-grade students in Baker, LA. The goal of this project is to increase student achievement through the use of the Singapore Primary Mathematics Curriculum and almost 100 hours of professional development each year. As the site coordinator, Roberts provides daily support to participating teachers. In addition, every two teachers are matched with a graduate student who co-teaches, helps with lesson planning, and answers content questions. During their hours of professional development, teachers learn math content across the grades, and have a chance to reflect on what they’ve learned and discuss what they don’t understand. The results have been promising: On a recent practice version of the state assessment, 45% of the 3rd grade students who began with the program 2-1/2 years ago passed. Compare this with test scores from the previous year of third grade students who were not part of the project: only 29% of these students passed. Roberts is delighted by the results, while at the same time working toward a 60% pass rate: "This project will afford the children we’re working with…to be able to aspire to careers in math and science-related fields that they otherwise might not have had the opportunity...These children are excited about learning mathematics." (Photo by Diane Madden of, left to right: Kristin Umland, Johnette Roberts, Lawrence Gray, Jim Madden and Hyman Bass)
The next presenter, Johnette Roberts, is the site coordinator of the Singapore Math Project for kindergarten through third-grade students in Baker, LA. The goal of this project is to increase student achievement through the use of the Singapore Primary Mathematics Curriculum and almost 100 hours of professional development each year. As the site coordinator, Roberts provides daily support to participating teachers. In addition, every two teachers are matched with a graduate student who co-teaches, helps with lesson planning, and answers content questions. During their hours of professional development, teachers learn math content across the grades, and have a chance to reflect on what they’ve learned and discuss what they don’t understand. The results have been promising: On a recent practice version of the state assessment, 45% of the 3rd grade students who began with the program 2-1/2 years ago passed. Compare this with test scores from the previous year of third grade students who were not part of the project: only 29% of these students passed. Roberts is delighted by the results, while at the same time working toward a 60% pass rate: "This project will afford the children we’re working with…to be able to aspire to careers in math and science-related fields that they otherwise might not have had the opportunity...These children are excited about learning mathematics." (Photo by Diane Madden of, left to right: Kristin Umland, Johnette Roberts, Lawrence Gray, Jim Madden and Hyman Bass)
The next presenter was Hyman Bass. He agreed with the other presenters: "what we’re about is not producing teachers who know a lot of mathematics, but trying to improve the learning of students in this country. It’s known that a teacher’s capacity is a major lever in improving that. [But while there are some small programs that have had positive local impacts,] we don’t really have a system in this country for professionally training teachers." In order to design an intervention that is potentially scalable, Bass and several colleagues realized they needed a better understanding of the mathematical knowledge needed for teaching, which they have termed MKT. In order to do this, they looked at "tons" of videos of teachers at work each day, documented a variety of mathematical events, analyzed the mathematical nature of those events and the type of knowledge they entailed, then tried to develop a theory that "distills the kind of mathematical knowledge [teachers] have to deploy in those situations." Their model separates this knowledge into two main categories. The first, which is itself divided into three subcategories, is pedagogical content knowledge. This type of knowledge combines knowledge of mathematics with knowledge of pedagogy: for example, knowing the best sequence to use to teach a topic. The other category—also divided into three subcategories—is subject matter knowledge. This includes "common" knowledge known by any person who uses math as well as "specialized" knowledge required only by math teachers, such as the ability to determine the mathematical legitimacy of a problem-solving approach. The fact that math teachers-in-training don’t get this "specialized" knowledge in a standard academic mathematics course or a methods course is a problem, Bass noted. And unless that changes, "we're going to see the outcomes that we've been witnessing for decades."
The final speaker was Kristin Umland who reflected on the question "What is mathematical reasoning in elementary mathematics?" One of the mathematical practices listed in the new Common Core Standards indicates that students must "construct viable arguments and critique the reasoning of others." Since students need to be able to do this, teachers must be able to do this as well, leading Umland to pose another question: How can teachers develop this knowledge and what would it look like? At this point, attendees were given a few minutes to consider, and then explain to another person, why 4 divided by 0 is undefined. When the time was up, Umland displayed some responses to this question from students in her pre-service course for elementary teachers. The good explanations "used the fact that division is defined in terms of multiplication." These explanations also either referred back to facts about multiplication, or used a model that related division to multiplication. Good models like these, Umland pointed out, can help students develop their mathematical reasoning and can "ratchet students up to the more abstract level of understanding that they’ll need later on." Mathematicians, working with elementary educators, are in a position to help "describe what reasoning in school mathematics can and should look like; create or improve materials that help kids develop their mathematical reasoning; and provide educational opportunities for teachers to develop their mathematical reasoning."
---Claudia Clark
SIGMAA on the Philosophy of Mathematics Guest Lecture: Will the real philosophy of mathematics please stand up?, Keith Devlin (Stanford University)
With his typical wit and insight, National Public Radio "math guy" Keith Devlin considered the meaning of the phrase "philosophy of mathematics," a discipline whose "main focus" over the past several thousand years has been on "how we know what we know about mathematics," i.e., proof. Yet many of the people that Devlin associates with mathematics, including engineers in a variety of fields, and people like Benoît Mandelbrot, Steve Wolfram, Larry Page and Sergey Brin—all of whose work has had a tremendous impact on people’s lives—"rarely stop to prove anything!" As Devlin sees it, "There’s a little bit of a disconnect if the philosophy of mathematics is focusing hugely on proof whereas there’s an awful lot of important mathematics going on that really isn’t about proof." In fact, Devlin pointed out, mathematical practice involves not only proving theorems: It also includes observation, analysis, generalization, inductive reasoning, computation, guesswork, and problem formulation, among other activities.
To get at this "disconnect," Devlin considered a definition of the philosophy of mathematics from the online Stanford Encyclopedia of Philosophy:
|
Whereas the [other sciences] acquire general knowledge using inductive methods, mathematical knowledge appears to be acquired in a different way, namely, by deduction from basic principles. [In addition], the theories of the natural sciences appear to be less certain and more open to revision than mathematical theories. |
Is this really true, he asked? While mathematicians understand proof to involve "a logically sound, complete argument that establishes the truth of something [that] starts with some assumptions," in reality, "obvious" steps must be omitted or most proofs would be prohibitively long. The reader can fill in these steps—in principle—but since this is impossible in practice, "when a mathematician publishes a proof, he or she is in effect issuing a challenge to the reader to try to show that it is wrong." But "isn’t that really the basis of scientific truth?" Devlin asked.
Devlin stressed that he is not trying to change the definition of proof. Rather, he says,
|
The question is: When do we know that an argument is a proof?…We need to be a little more honest about what that means. Because the real question is, on what basis do we determine, as a community, that a claimed proof is correct? |
For Devlin, it is a matter of "certification by the profession…using rational thought to evaluate available evidence." In conclusion, Devlin’s "rallying cry" is that the philosophy of mathematics should "look at the whole nature of mathematical practice," including experimental methods and evaluating proofs, not just proving theorems.
---Claudia Clark
Read more of events at the Joint Meetings in Adriana Salerno's experiences on the JMM 2011 blog.

